课程内容主要分为两个部分:算法分析和算法设计。算法分析是理论研究,研究计算机程序的性能和资源利用,尤其关注性能,也考量其他方面如通信、存储(内存、磁盘)等
排序算法例子
输入一组序列 ,按照从小到大的顺序排列后输出
使用插入排序算法来完成,伪代码如下1
2
3
4
5
6
7For j=2 to n
key = A[j]
i = j-1
while i>0 and A[i]>key
A[i+1] = A[i]
i -= 1
A[i+1] = key
该算法有两层循环,外层循环j从2到n递增,内层循环i从j-1到0递减。任意一次循环前的情况如图所示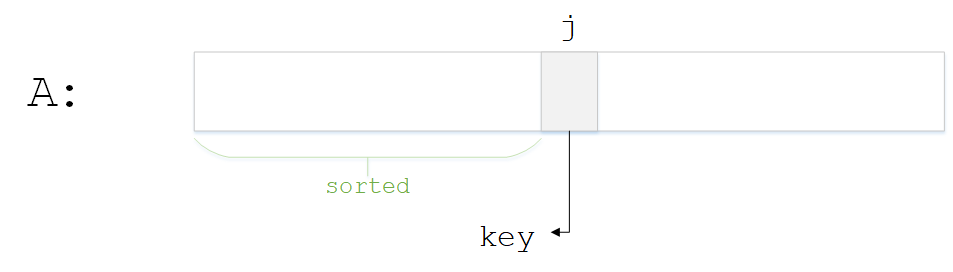
关键点如下
- 将数组j位置的元素提取出来,记作key
- 0到j-1位置的元素为已排列sorted
- 循环的目的就是使sorted部分增长1
循环步骤如图所示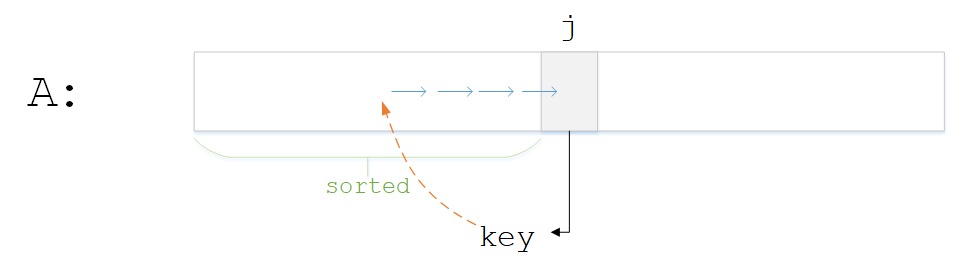
做法是一步步将前一个元素拷贝到后一个位置,直到找到key值的合适位置,插入进去
排序算法分析
运行时间
算法的运行时间取决于很多因素
- 输入本身 如果输入本身已经是排好序的或者部分排好序的,剩余的工作就很少;而最坏的情况是逆序,所有的元素都要重新调整
- 输入规模 将运行时间看作数据规模的函数
- 运行时间的上界 运行时间不会超过的某个值,这代表对用户的一种承诺;如果关注运行时间最快是多少是没有意义的,因为一个很烂的算法在输入本身已经排好序的情况下也可以很快
各种类型的分析
- 最坏情况分析 通常最关注这个,定义$T(n)$为输入规模为$n$时的最长运行时间,
- 平均情况分析 这里$T(n)$是输入规模$n$之下所有可能输入的期望时间,而计算期望,必须假定或者给出输入的统计分布(如均匀分布、正态分布等)
- 最好情况分析 这是一种假象,没啥用
那么,插入排序的最坏情况消耗多少时间?首先取决于运行该算法的计算机,计算能力是多少。当比较算法时,比较的是相对速度,即在相同的计算机上作比较。当然,也会关心其绝对速度,一个算法,无论在什么样的机器上,其能力都可以用一种形式表示,那就是算法的大局观——渐进分析
算法大局观——渐进分析
渐进分析的基本观点
- 忽略掉依赖于机器的常量,
- 不去检查实际的运行时间
- 关注运行时间的增长
定义$\Theta$符号,表示弃去低阶项,忽略常数因子。例如公式为$3n^{3}+90n^{2}-5n+6046$,最高阶是3阶,因此2阶项和1阶项都去掉,常数项也去掉,则该公式为$\Theta(n^{3})$
当$n \to +\infty$,可知总是存在一个$n$,使得$\Theta(n^{2})$的算法优于$\Theta(n^{3})$的算法,无论其他低阶项和常数项是什么;即使在一台慢速机器上运行$\Theta(n^{2})$,而在快速机器上运行$\Theta(n^{3})$,也不影响$\Theta(n^{2})$超过$\Theta(n^{3})$
$\Theta$符号的好处在于可以满足对相对速度和绝对速度的双重比较要求,因为无论在什么计算机平台上都能实现这一点,在不同平台上也许只差一个常数因子,但随着输入规模变大,渐进结果是准确的,如图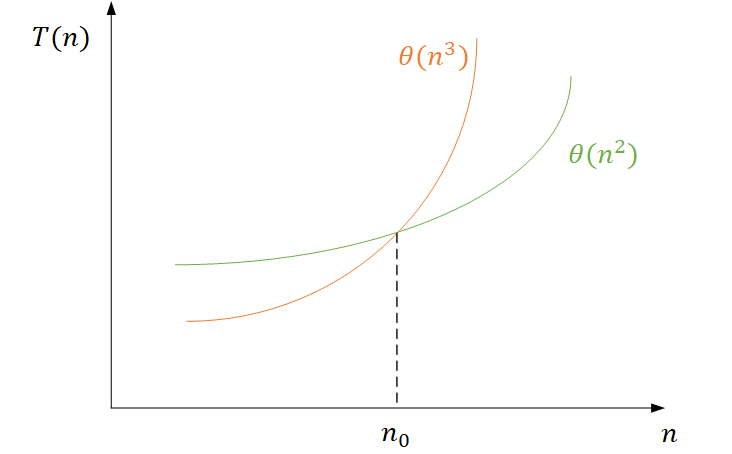
总会存在一个$n{0}$,当$n > n{0}$时,$\Theta(n^{2})$比$\Theta(n^{3})$的时间开销更小。但是有些时候,$n_{0}$的值过大,大到计算机无法运行该算法,这也是某些情况下对相对低速的算法也感兴趣的原因,因为低速算法尽管用渐进的视角来看,最终可能比较慢,但是让然可以在合理输入范围内运行更快。因此需要在数学理论和工程直觉之间做权衡
排序算法的最坏情况
最坏情况是输入是逆向排序,每次循环都要把所有元素移动一次。假设每一条代码指令或原子操作都耗费某固定常数时间,而这个常数是多少无关紧要。外层循环从$j=2$到$n$,对于j的每一次取值,循环体的执行耗时应该是$j$乘以某个常数,则耗时为$\Theta(j)$。因此排序算法的总时间消耗为
\begin{equation}
T(n) = \sum_{i=1}^{n} \Theta(j)
\end{equation}
如何简化该公式呢?这是一个求和表达式,具体来说是等差数列求和,等差数列求和公式为
\begin{equation}
S(n) = na_{1} + \frac{n(n-1)}{2} d
\end{equation}
最高阶次为2次,省略掉常数项和低阶项,等于$\Theta(n^{2})$,即
\begin{equation}
T(n) = \sum_{i=1}^{n} \Theta(j) = \Theta(n^{2})
\end{equation}
因此,对于较小的$n$,插入排序的速度还可以,但是$n$足够大时,插入排序效率就比较低了
并归排序
对于数组A[1...n]的并归排序,有3个步骤
- 如果
n=1,认为已经排好序了 - 递归地对A[1到n/2向上取整]和A[n/2向下取整到n]这两部分排序
- 把排好序的两个表并归
关键的子程序在于并归,下图中是两个已经排好序的数组,首先判断两张表中最小元素是多少,最小元素一定在两张表之首;然后将最小的元素拿出来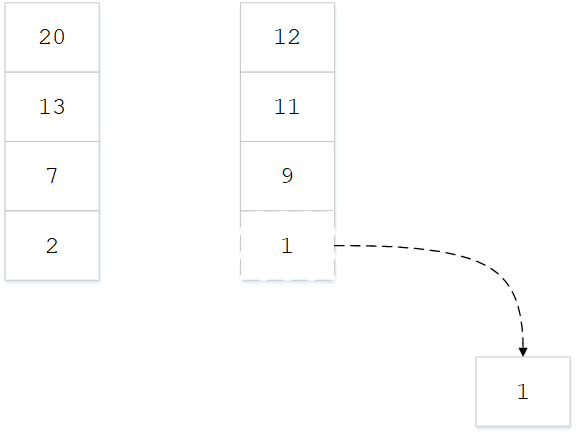
重复以上步骤,每次从两个表头取出最小的元素排在新数组的后面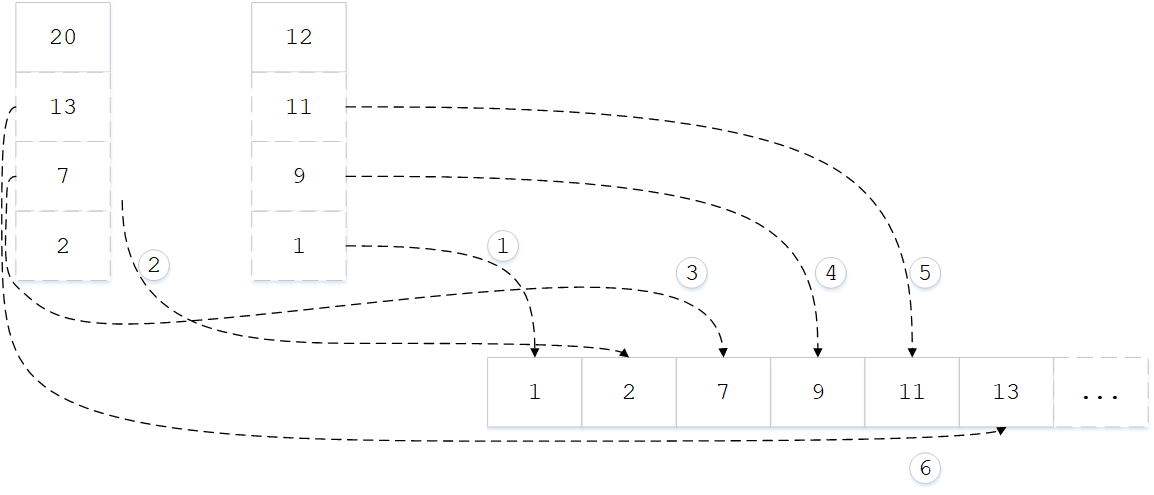
分析性能
并归算法的$T(n)$是多少?该算法的3个步骤中,第1步只需要常数时间;第2步可以描述成
\begin{equation}
T(n) = T(n/2向下取整) + T(n/2向上取整) = 2T(n/2)
\end{equation}
第3步并归两张已排序好的表,耗时为$\Theta(n)$
综上,并归排序的总耗时$T(n)$为
该表达式用递归树方法分析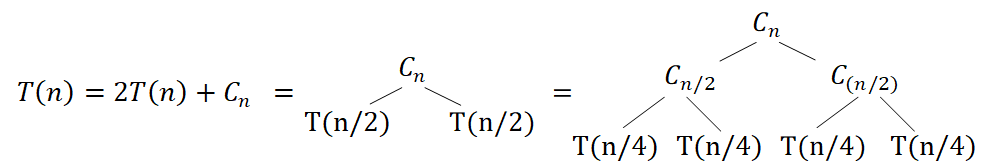
最终可以分解为一个递归树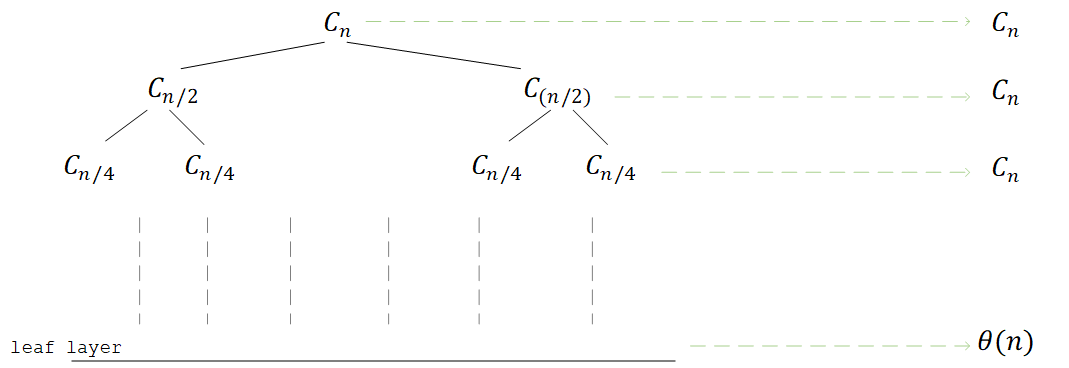
树高为$\log{2}n$,叶子节点最大为$n$,将树上所有层级耗时相加,总和为
\begin{equation}
C{n} \log{2}n + \Theta(n) = \Theta(n\log{2}n)
\end{equation}
$\Theta(n\log_{2}n)$比$\Theta(n^{2})$快