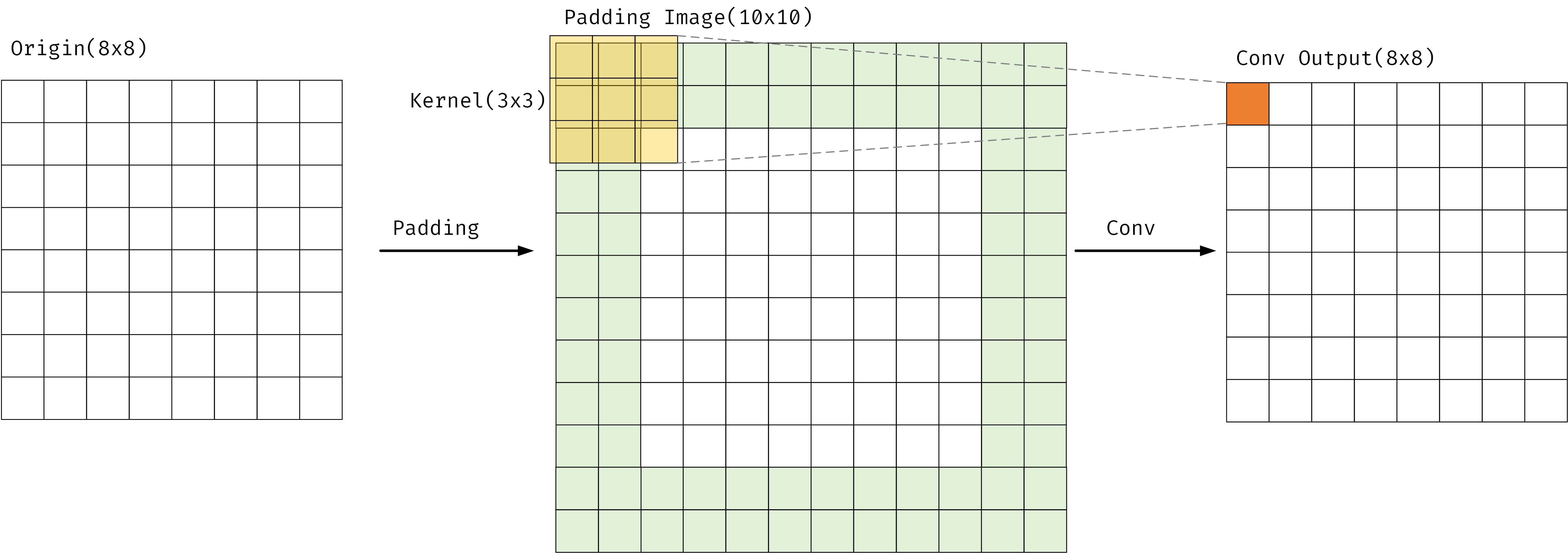
卷积操作在图像处理中非常重要，大部分空域滤波都需要进行卷积操作。卷积运算是在卷积核(kernel)与图像邻域之间进行的一种变换操作，并以图像为参照系，逐像素移动卷积核的中心，从左向右，从上到下，最终获得经过卷积处理后的图像

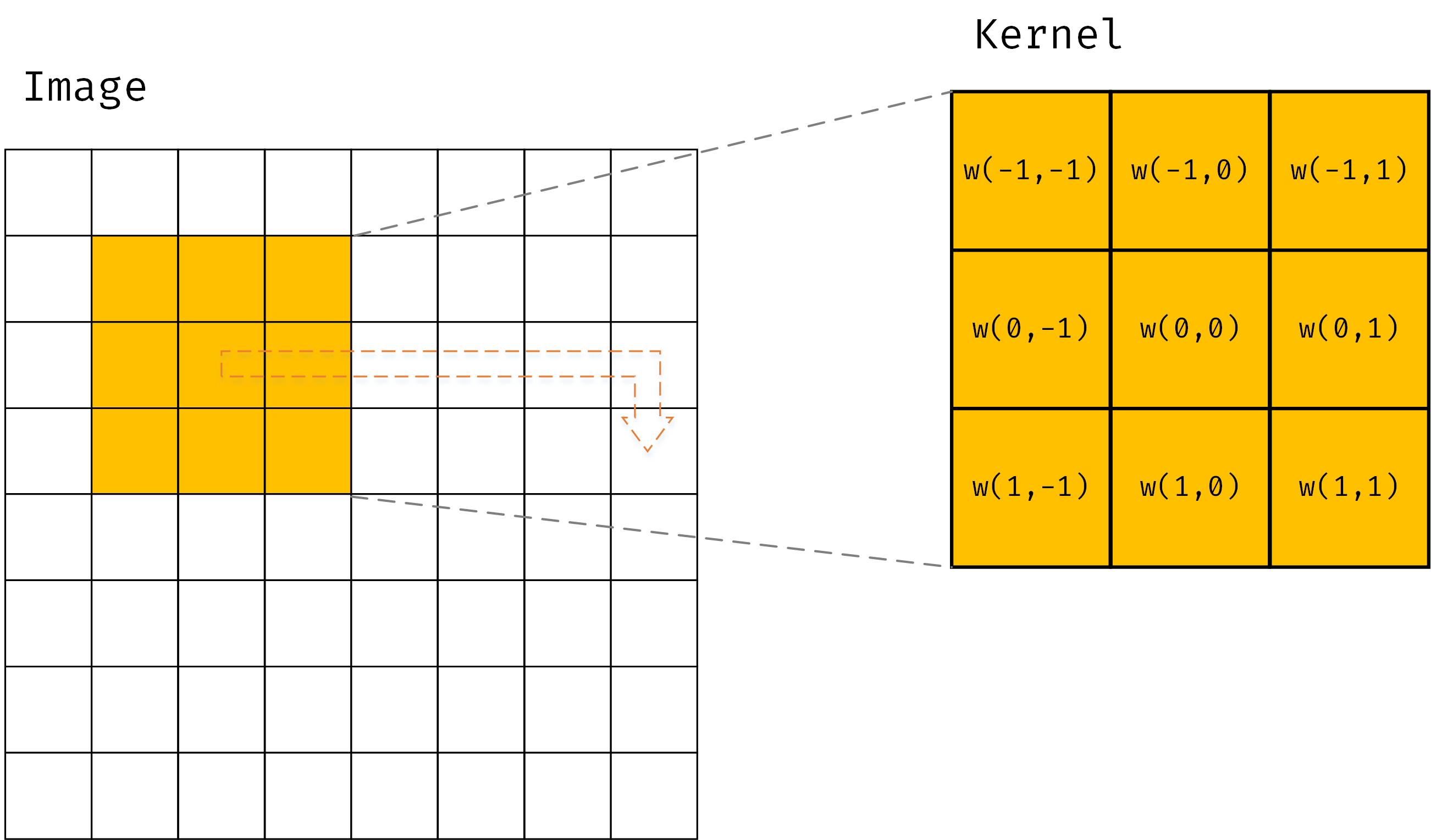
空间相关与卷积

严谨的说，以上对于卷积操作的描述并不准确，这实际上是空间相关(Spatial Correlation)的过程，大小为$m \times n$的核$w(s,t)$与图像$f(x,y)$的相关$(w\bigstar f)(x,y)$定义为

\begin{equation}
(w \bigstar f)(x,y) = \sum{s=-a}^{a}\sum{t=-b}^{b}w(s,t)f(x+s, y+t)
\end{equation}

其中，$a=(m-1)/2$，$b=(n-1)/2$，且$m、n$都为奇数。相关运算存在核旋转特性，以下进行示例说明

定义一个$5 \times 5$的测试图像im，仅在中心像素点im[2][2]值为1，其余像素值全0，将其与一个$3 \times 3$的kernel进行运算，kernel的值为0-9顺序排列，可以观察到相关运算的结果是产生了一个旋转180°的kernel

首先定义相关运算

import numpy as np

# define kernel calculate
def sum_kernel(matrix, kernel):
    n = len(kernel)
    sum = 0
    for i in range(n):
        for j in range(n):
            sum += matrix[i,j]*kernel[i,j]
    return sum

# define correlation calculate
def image_correlation(im, kernel):
    n = len(kernel)
    # padding size: 2*(kernelsize - 1)
    im_padding = np.zeros((im.shape[0]+2*(n-1), im.shape[1]+2*(n-1)))
    # im data copy to padding im
    im_padding[(n-1):(n+im.shape[0]-1), (n-1):(n+im.shape[1]-1)] = im
    im_conv = np.zeros((im_padding.shape[0]-n+1, im_padding.shape[1]-n+1))
    for i in range(im_padding.shape[0]-n+1):
        for j in range(im_padding.shape[1]-n+1):
            neighbor = im_padding[i:i+n, j:j+n]
            im_conv[i, j] = conv2d_kernel(neighbor, kernel)
    pos = int((n-1)/2)
    im_new = im_conv[pos:(pos+im.shape[0]), pos:(pos+im.shape[1])]
    return im_new

创建测试图像数据

1
2
3

im = np.zeros((5, 5))
im[2,2] = 
print(im)

[[0. 0. 0. 0. 0.]
 [0. 0. 0. 0. 0.]
 [0. 0. 1. 0. 0.]
 [0. 0. 0. 0. 0.]
 [0. 0. 0. 0. 0.]]

创建kernel

1 2	kernel = np.array([[1,2,3], [4,5,6], [7,8,9]]) print(kernel)

1
2
3

[[1 2 3]
 [4 5 6]
 [7 8 9]]

进行相关运算

1 2	im_new = image_correlation(im, kernel) print(im_new)

[[0. 0. 0. 0. 0.]
 [0. 9. 8. 7. 0.]
 [0. 6. 5. 4. 0.]
 [0. 3. 2. 1. 0.]
 [0. 0. 0. 0. 0.]]

因此，在进行卷积运算时，需要将卷积核旋转180°，卷积运算的定义为

\begin{equation}
(w \ast f)(x,y) = \sum{s=-a}^{a}\sum{t=-b}^{b}w(s,t)f(x-s, y-t)
\end{equation}

如果卷积核是关于中心对称时，相关和卷积运算结果相同，也就不需要进行旋转了

Padding

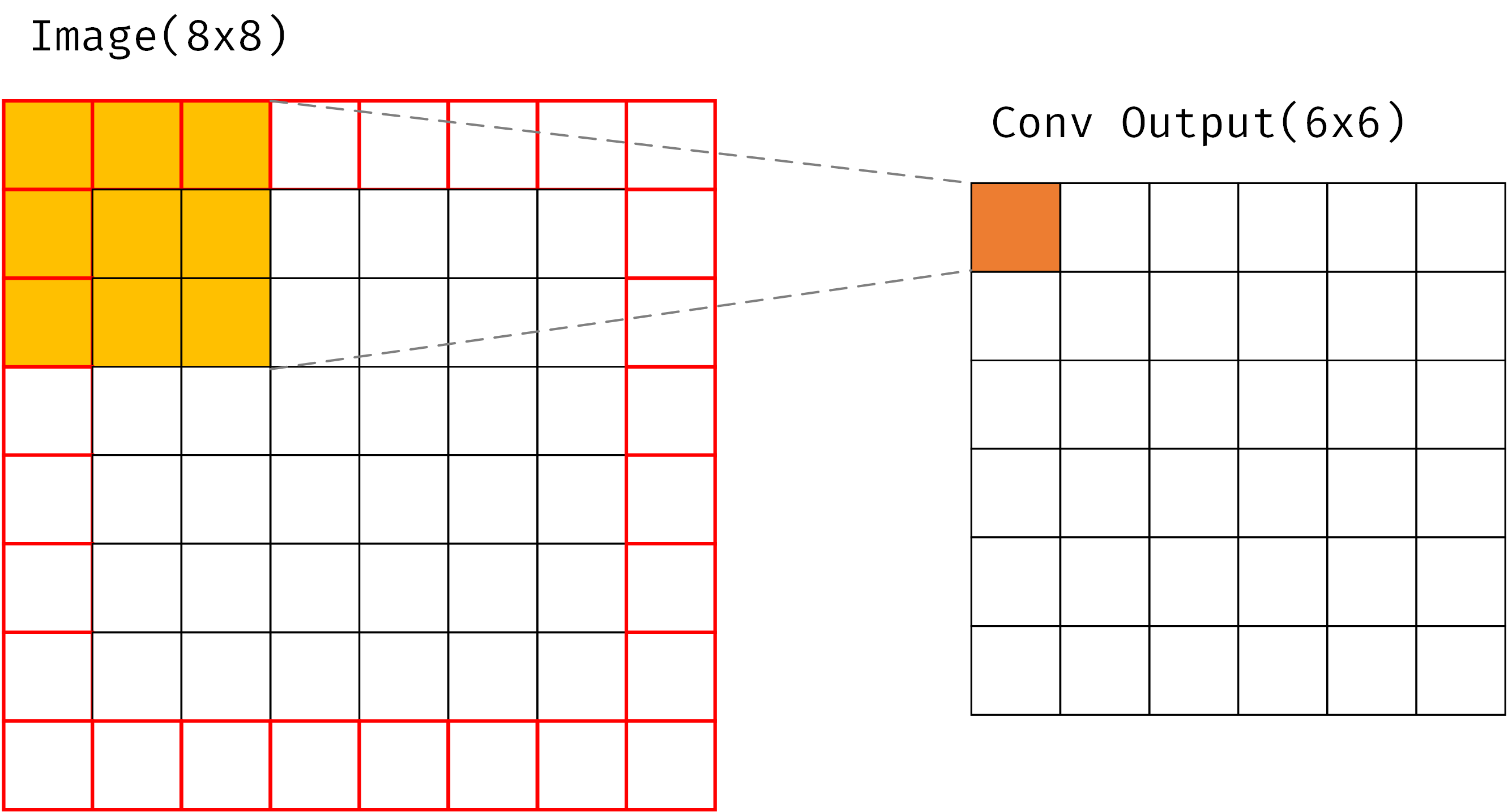
以$3 \times 3$的卷积核为例，由于在像素$f(x,y)$处的卷积运算需要$f(x-1,y-1),f(x+1,y+1)$等邻域的值，卷积核只能在图像边界内与边界重合移动，如果不进行填充操作，边界处的像素无法计算卷积(红色边框的像素)，卷积最终得到的图像大小将小于原始图像

因此如果希望卷积后的图像大小与原始图像一致，就需要进行边界填充操作。大小为$n \times n$的卷积核与大小为$m \times m$的图像进行卷积，每个边需要向外填充$(n-1)$的像素，整个填充后图像大小为$m+2(n-1)$。如下图，左侧为$8 \times 8$的原始图像，填充图像为$10 \times 10$大小，绿色为填充的部分，每边向外填充了2个宽度的像素，经过卷积运算后大小为$8 \times 8$