何凯明等人在2015年的”Deep Residual Learning for Image Recognition”这篇论文中提出了Resnet网络架构,是CNN图像领域一个重要的里程碑,后续多年直至如今在图像分类领域仍然有超过半数的网络使用着Resnet或其变种。Resnet提出了一种残差块结构,解决了在深度神经网络中由于梯度消失或梯度爆炸导致的网络难以训练的问题,以及更深的层次反而导致网络性能下降问题
深度神经网络的训练问题
梯度爆炸和梯度消失
深度神经网络可以设置很深的层次结构,深层结构可以得到更高层级的语义特征。但是随着网络层数越来越深,训练过程会出现梯度消失和梯度爆炸的问题,训练难以进行
梯度消失和梯度爆炸是同一个问题,主要原因是由于SGD反向传播是以链式法则进行梯度的反向连乘传导,而随着网络层数加深,梯度将以指数形式传播,很容易将梯度大幅度放大或缩小,从而导致梯度消失或爆炸
在这篇文章发布之前,业界通常的做法主要有以下两方面
使用较好的权重初始化方式,让权重分布更合理
使用BatchNormalization,在层与层之间做正则化,避免出现特别大或特别小的层
使用了这些技术之后,确实能够在一定程度上解决训练不收敛的问题
网络越深性能反而下降
解决了训练不收敛问题后,仍然存在的一个问题是,随着网络层数的加深,性能不增反降
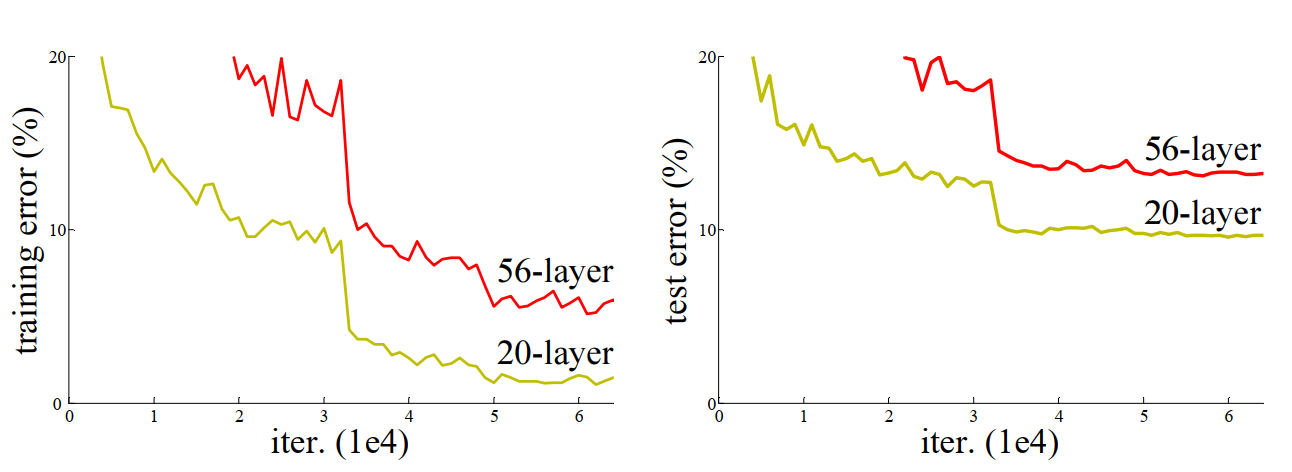
上图是文章在CIFAR-10数据集上分别以一个20层和56层深度的模型进行训练,并绘制训练误差和测试误差曲线。从图中可以看出,56层的模型训练误差和测试误差反而更高。这种现象并不是发生了过拟合,而是网络训练不动了
假设有一个层数较浅的网络shallower和一个在shallower基础上增了若干层后较深的网络deeper。如果在shallower网络性能还不错的情况下,理论上deeper网络最差也是和shallower一样,不应该比shallower更差,因为可以将deeper和shallower相同层数的层看作是shallower的一个拷贝,即图中deeper网络中黄色层部分的权重参数和shallower完全一致,而将剩余的蓝色部分看作是一个identity mapping,即这些层什么都不干,输入是什么,输出还是什么,这样的话,deeper网络的性能和shallower性能应该完全相同
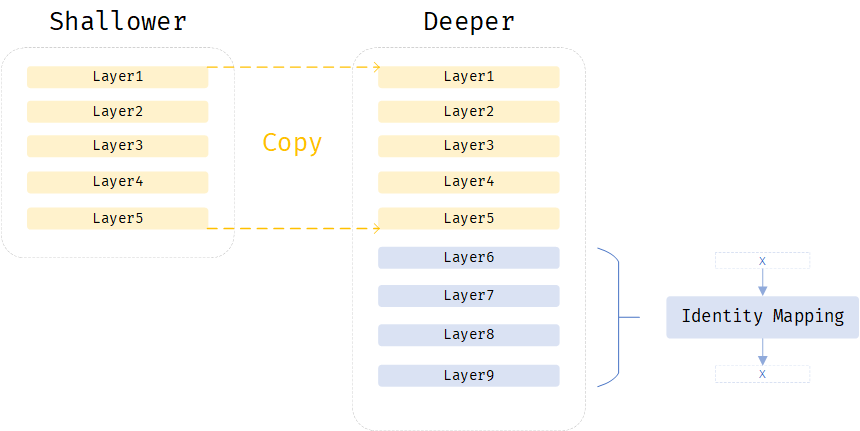
但是SGD无法学习和找到这样的权重
Resnet网络架构
Residual结构
Resnet显式的构造了一个identity mapping,使得更深的网络不会比浅层网络的性能更差。假设有一个网络,现在给它增加一个层,假设之前层的输出是$x$,按照正常的方式处理,新增加的层可以看作是学习一个$H(x)$的映射,如下图所示
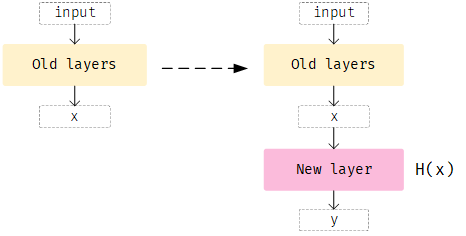
而现在,不让新增加的层直接学习$H(x)$,而是学习一个$F(x)=H(x)-x$的映射,其含义是新增加的层不要直接从前面的网络已经学习到的输出$x$去再学习,而是学习前面网络已经学到的东西和label之间的残差。这样使得新增加的整个结构Residual学习的映射变换为$H(x) = F(x)+x$。如下图所示,新增加的层New layer,New layer本身学习的是$F(x)$,而Residual结构是New layer的输出加前面网络的输出$x$
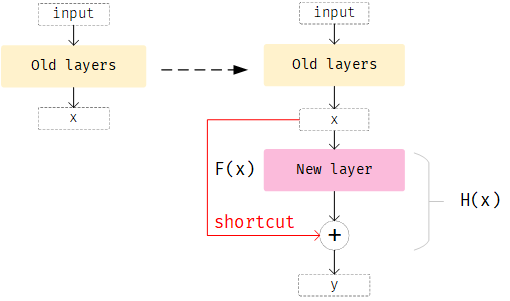
Residual结构和正常增加一个层唯一需要变动的就是增加了一个上层网络输出$x$和新增层输出$F(x)$的shortcut connection,如图中红色箭头部分。这个结构不会增加任何要学习的参数,也不会让计算复杂的变高
文章指出,这种Residual结构的网络非常容易优化,而且随着网络层数越深,网络性能越好
残差连接shape问题
当残差连接的输入和输出shape不相等时,文章提供了两种将输入和输出变换为相同shape的方法
输入和输出都用0补充到相同shape
使用一个1x1 stride=2的卷积,将输入和输出shape匹配
文章在实验中对比了这两种方案,使用第二种方案效果更好
不同版本的Resnet
文章给出了以下5种不同大小的Resnet模型
Resnet18
Resnet34
Resnet50
Resnet101
Resnet152
不同大小的Resnet版本后跟的数字表示的是网络的层数,例如Resnet18表示整个网络有10层。5个版本网络架构的第一层7x7的卷积层、第二层的maxpool和最后一层全连接层都是相同的,不一样的是中间的残差块Block部分,各个残差块之间使用了残差连接。这里有两种类型的残差块Basic和Bottleneck,下图中用不同颜色区分开了,Resnet18和Resnet34使用的是一种残差块,而Resnet50、Resnet101和Resnet152使用的是另一种残差块

当网络层数为18和34时,使用的残差块是Basic,大于等于50层后,使用的残差块是Bottleneck
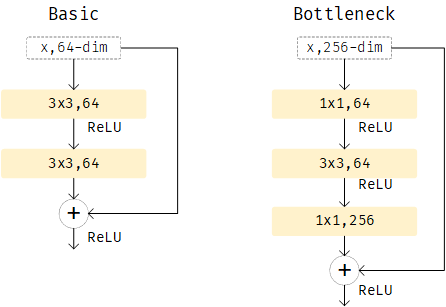
当网络层数更多时,feature的维度比较大,能够学习到更多特征,为了降低计算复杂度,在Bottleneck中,使用了(1x1, 64)的卷积层将256维的feature投影回64维,经过(3x3, 64)卷积后,再经过(1x1, 256)的卷积投影回256维度
这里需要注意,在一种Resnet版本种,每个Block表示一个残差块组,一个组中的残差块使用相同的特征维度在残差块之间传递。图中Block旁边标识了该Block中有多少个重复的残差块。不同残差块组的特征维度是不同的,Resnet18和Resnet34的特征维度从上到下分别是64、128、256、512,Resnet50、Resnet101和Resnet152的特征维度分别是256、512、1024、2048
Resnet实验结果
文章对比了两种相同层数(18和34层)的网络版本,plain-18和plain-34是未使用残差结构的网络,ResNet-18和ResNet-34是使用了残差结构的网络。下图显示了测试对比结果,图中较粗的曲线是验证误差,较细的曲线是训练误差
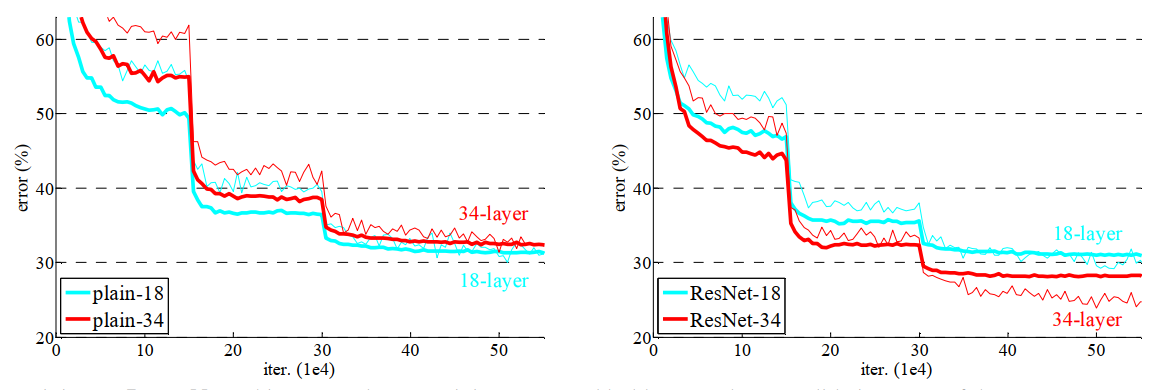
对比plain和ResNet的结果可以看出,使用了残差结构的网络误差低于未使用残差结构的网络,且更深的层数能够取得更好的性能,训练时收敛速度也更快
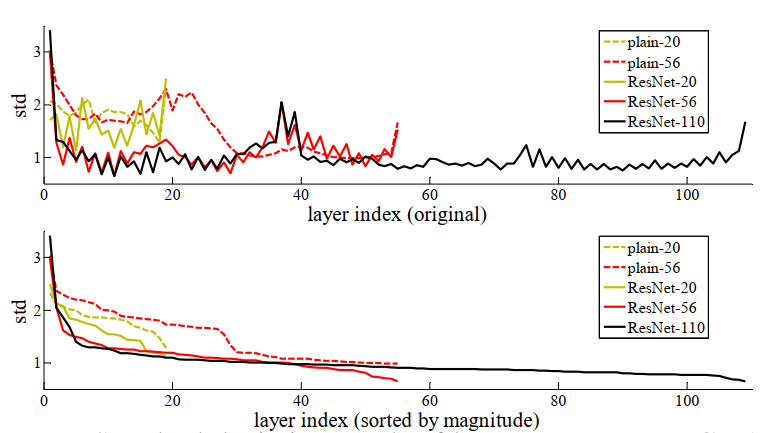
文章在CIFAR-10上还做了一个110层模型的实验,对比了使用残差块和未使用残差块模型中训练收敛时不同层是否还在起作用,实验表明Resnet网络在前若干层已经训练收敛后,后面的层不会起太多作用,这样使得网络不会因为层的加深反而性能变差,而未使用残差块的网络较深的层仍然在其比较大的作用
原理
正常的网络假设是$g(x)$,在其后增加一些层,则网络变为$f(g(x))$,根据链式法则,对该网络对$x$求导为
\begin{equation}
\frac{df(g(x))}{dx} = \frac{df(g(x))}{dg(x)} \cdot \frac{dg(x)}{dx}
\end{equation}
因为深层网络的梯度链是很长的连乘,当网络逐渐收敛时,梯度本身比较小,长的连乘很容易导致最终输出的梯度为0。在Resnet的情况下,增加一些层后,网络变为$f(g(x)+x)$,对$x$求导变为
\begin{equation}
\frac{df(g(x)+x)}{dx} = \frac{df(g(x))}{dg(x)} \cdot \frac{dg(x)}{dx} + \frac{dg(x)}{dx}
\end{equation}
多出来的$\frac{dg(x)}{dx}$这一项会使得整个梯度变大一些,更容易训练