DIP-boxfilter快速窗口求和

发表于 | 分类于 ， |

在很多图像处理任务中，需要对局部图像数据进行窗口运算，许多运算都需要获得局部区域像素的均值和方差，这些计算都离不开求和运算。我在研究引导滤波时，发现何凯明在其提供的引导滤波matlab参考代码中，使用了boxfilter的快速计算方法，能够以$O(1)$的时间复杂度对矩阵进行局部快速求和运算

本文对以python代码为例，对boxfilter的运算细节进行可视化分析，使读者对整个计算过程有一个直观的感受，然后将正常的卷积局部求和操作与boxfilter进行性能比较

运算过程分析

首先对boxfilter的输入和输出进行说明，boxfilter的输入是要计算局部窗口和的整幅图像$I$，输出是与输入图像尺寸相同的图像$F$，输出图像某个像素的值$F(x,y)$是以$I(x,y)$为中心的一个窗口内所有像素值的和，窗口在图像上滑动，与卷积操作类似，窗口大小也是一个输入参数，一般以窗口半径$r$来表示。下图是输入与输出关系的示意图

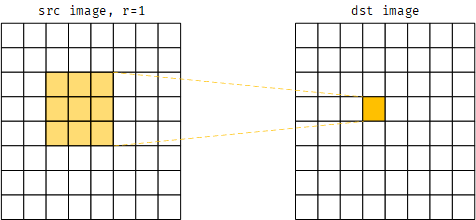
输出图像是将一个窗口的求和作用于输入图像的结果，上图中窗口半径为1，则窗口尺寸为3x3，图中输入图像中的黄色3x3区域即为一个窗口，该窗口内输入图像的像素之和对应于输出图像的黄色像素

下面将详细介绍整个快速计算的过程，引入依赖库

1
import numpy as np

定义一个8x8的二维单位矩阵作为输入图像，定义窗口半径为1，则kernel size为3x3，创建一个与输入图像相同shape的0矩阵

1
2
3
4
5
r = 1
imSrc = np.ones((8, 8))
I = imSrc.copy()
imDst = np.zeros(I.shape)
h, w = I.shape

打印imSrc

1
print(imSrc)
1
2
3
4
5
6
7
8
[[1. 1. 1. 1. 1. 1. 1. 1.]
 [1. 1. 1. 1. 1. 1. 1. 1.]
 [1. 1. 1. 1. 1. 1. 1. 1.]
 [1. 1. 1. 1. 1. 1. 1. 1.]
 [1. 1. 1. 1. 1. 1. 1. 1.]
 [1. 1. 1. 1. 1. 1. 1. 1.]
 [1. 1. 1. 1. 1. 1. 1. 1.]
 [1. 1. 1. 1. 1. 1. 1. 1.]]

打印imDst

1
print(imDst)
1
2
3
4
5
6
7
8
[[0. 0. 0. 0. 0. 0. 0. 0.]
 [0. 0. 0. 0. 0. 0. 0. 0.]
 [0. 0. 0. 0. 0. 0. 0. 0.]
 [0. 0. 0. 0. 0. 0. 0. 0.]
 [0. 0. 0. 0. 0. 0. 0. 0.]
 [0. 0. 0. 0. 0. 0. 0. 0.]
 [0. 0. 0. 0. 0. 0. 0. 0.]
 [0. 0. 0. 0. 0. 0. 0. 0.]]

对输入图像进行行方向的累加求和，并打印

1
2
I = np.cumsum(I, 0)
print(I)
1
2
3
4
5
6
7
8
[[1. 1. 1. 1. 1. 1. 1. 1.]
 [2. 2. 2. 2. 2. 2. 2. 2.]
 [3. 3. 3. 3. 3. 3. 3. 3.]
 [4. 4. 4. 4. 4. 4. 4. 4.]
 [5. 5. 5. 5. 5. 5. 5. 5.]
 [6. 6. 6. 6. 6. 6. 6. 6.]
 [7. 7. 7. 7. 7. 7. 7. 7.]
 [8. 8. 8. 8. 8. 8. 8. 8.]]

将累加求和后的矩阵2、3两行复制到imDst的第1、2行，并打印(本文中描述第n行，n从1开始)

1
2
imDst[:r+1, :] = I[r:2*r+1, :]
print(imDst)
1
2
3
4
5
6
7
8
[[2. 2. 2. 2. 2. 2. 2. 2.]
 [3. 3. 3. 3. 3. 3. 3. 3.]
 [0. 0. 0. 0. 0. 0. 0. 0.]
 [0. 0. 0. 0. 0. 0. 0. 0.]
 [0. 0. 0. 0. 0. 0. 0. 0.]
 [0. 0. 0. 0. 0. 0. 0. 0.]
 [0. 0. 0. 0. 0. 0. 0. 0.]
 [0. 0. 0. 0. 0. 0. 0. 0.]]

这一步的过程如下图所示

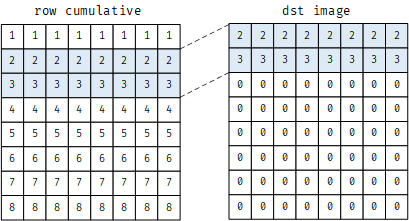
该操作的含义是当求和窗口未完全在图像内部时的图像边缘求和处理

然后将累加矩阵的第4到8行减去1到5行的结果复制到imDst的第3到7行，并打印

1
2
imDst[r+1:h-r, :] = I[2*r+1:, :] - I[:h-2*r-1, :]
print(imDst)
1
2
3
4
5
6
7
8
[[2. 2. 2. 2. 2. 2. 2. 2.]
 [3. 3. 3. 3. 3. 3. 3. 3.]
 [3. 3. 3. 3. 3. 3. 3. 3.]
 [3. 3. 3. 3. 3. 3. 3. 3.]
 [3. 3. 3. 3. 3. 3. 3. 3.]
 [3. 3. 3. 3. 3. 3. 3. 3.]
 [3. 3. 3. 3. 3. 3. 3. 3.]
 [0. 0. 0. 0. 0. 0. 0. 0.]]

示意图如下

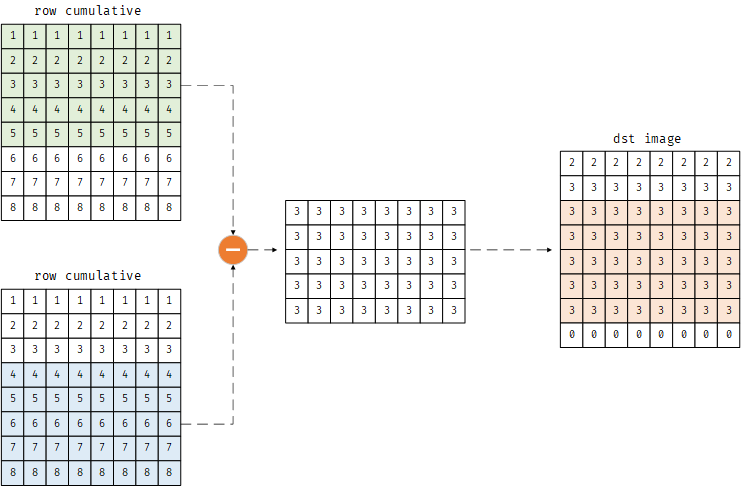
然后将累加矩阵的最后一行与第6行相减，结果复制到imDst的第8行

1
2
imDst[h-r:,:]=np.matlib.repmat(I[h-1,:],r,1)-I[h-2*r-1:h-r-1,:]
print(imDst))
1
2
3
4
5
6
7
8
[[2. 2. 2. 2. 2. 2. 2. 2.]
 [3. 3. 3. 3. 3. 3. 3. 3.]
 [3. 3. 3. 3. 3. 3. 3. 3.]
 [3. 3. 3. 3. 3. 3. 3. 3.]
 [3. 3. 3. 3. 3. 3. 3. 3.]
 [3. 3. 3. 3. 3. 3. 3. 3.]
 [3. 3. 3. 3. 3. 3. 3. 3.]
 [2. 2. 2. 2. 2. 2. 2. 2.]]

示意图如下

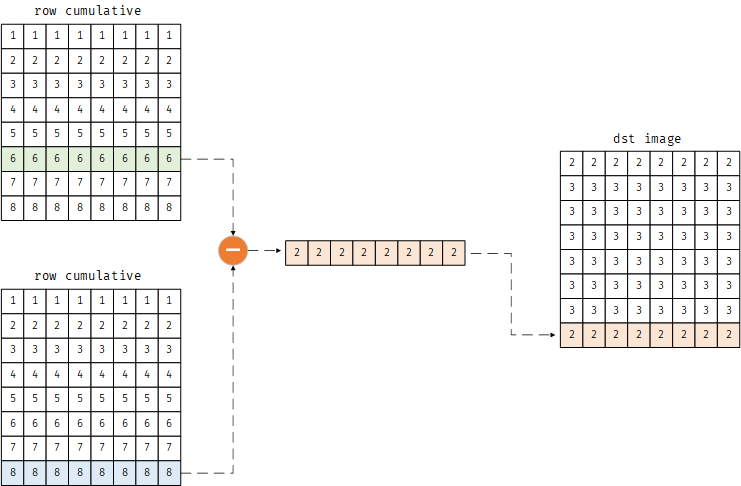
这里使用的repmat含义是将累加矩阵的最后一行复制为一个r行的矩阵，因为r为1，因此不进行任何操作。如果r大于1时，在下边缘处的窗口计算，就需要补一行

至此，行处理完成，接下来进行列处理。首先是对输入图像进行列方向的累加求和，并打印

1
2
I = np.cumsum(imDst, 1)
print(I)

注意列方向进行累加求和是在行方向累加求和基础上做的

1
2
3
4
5
6
7
8
[[ 2.  4.  6.  8. 10. 12. 14. 16.]
 [ 3.  6.  9. 12. 15. 18. 21. 24.]
 [ 3.  6.  9. 12. 15. 18. 21. 24.]
 [ 3.  6.  9. 12. 15. 18. 21. 24.]
 [ 3.  6.  9. 12. 15. 18. 21. 24.]
 [ 3.  6.  9. 12. 15. 18. 21. 24.]
 [ 3.  6.  9. 12. 15. 18. 21. 24.]
 [ 2.  4.  6.  8. 10. 12. 14. 16.]]

然后将累加和的前第2、3列拷贝到imDst的第1、2列

1
2
imDst[:,:r+1] = I[:,r:2*r+1]
print(imDst)
1
2
3
4
5
6
7
8
[[4. 6. 2. 2. 2. 2. 2. 2.]
 [6. 9. 3. 3. 3. 3. 3. 3.]
 [6. 9. 3. 3. 3. 3. 3. 3.]
 [6. 9. 3. 3. 3. 3. 3. 3.]
 [6. 9. 3. 3. 3. 3. 3. 3.]
 [6. 9. 3. 3. 3. 3. 3. 3.]
 [6. 9. 3. 3. 3. 3. 3. 3.]
 [4. 6. 2. 2. 2. 2. 2. 2.]]

示意图如下

然后将累加和的第4到8列减去1到5列，结果拷贝到imDst的第3到7列

1
2
imDst[:,r+1:w-r] = I[:,2*r+1:]-I[:,:w-2*r-1]
print(imDst)
1
2
3
4
5
6
7
8
[[4. 6. 6. 6. 6. 6. 6. 2.]
 [6. 9. 9. 9. 9. 9. 9. 3.]
 [6. 9. 9. 9. 9. 9. 9. 3.]
 [6. 9. 9. 9. 9. 9. 9. 3.]
 [6. 9. 9. 9. 9. 9. 9. 3.]
 [6. 9. 9. 9. 9. 9. 9. 3.]
 [6. 9. 9. 9. 9. 9. 9. 3.]
 [4. 6. 6. 6. 6. 6. 6. 2.]]

示意图如下

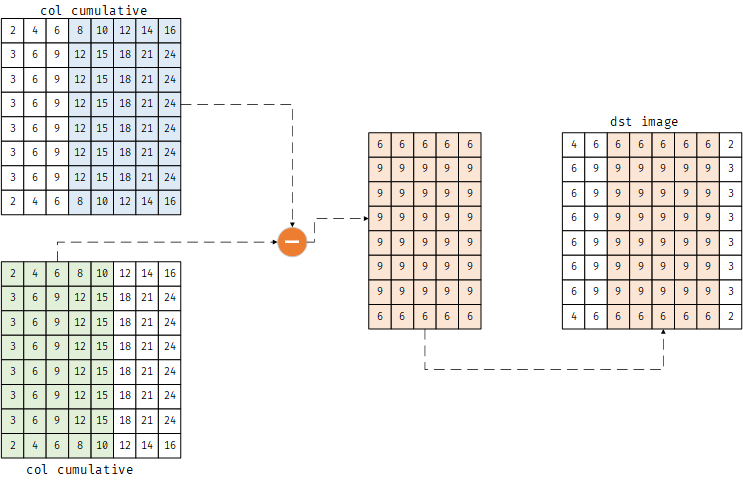
最后将累加和第8列减去第6列，结果复制到imDst的第8列

1
2
imDst[:,w-r:] = np.matlib.repmat(I[:,w-1].reshape(-1,1),1,r)-I[:,w-2*r-1:w-r-1]
print(imDst)
1
2
3
4
5
6
7
8
[[4. 6. 6. 6. 6. 6. 6. 4.]
 [6. 9. 9. 9. 9. 9. 9. 6.]
 [6. 9. 9. 9. 9. 9. 9. 6.]
 [6. 9. 9. 9. 9. 9. 9. 6.]
 [6. 9. 9. 9. 9. 9. 9. 6.]
 [6. 9. 9. 9. 9. 9. 9. 6.]
 [6. 9. 9. 9. 9. 9. 9. 6.]
 [4. 6. 6. 6. 6. 6. 6. 4.]]

示意图如下

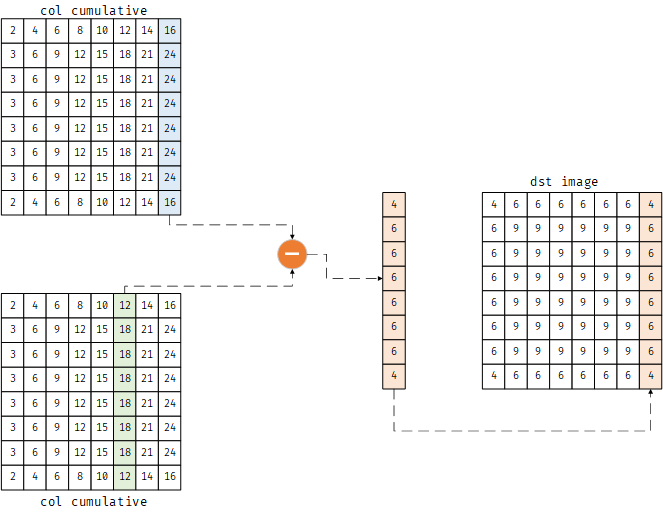
这个结果是否正确呢？可以选取几个局部窗口位置计算一下，可以看到，结果确实是正确的

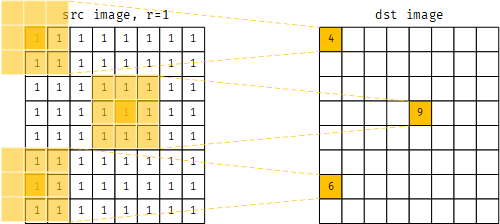
整合之后的boxfilter函数如下

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
def boxfilter(im, r):
    I = im.copy()
    imDst = np.zeros(I.shape)
    h, w = I.shape
    
    # row process
    I = np.cumsum(I, 0)
    imDst[:r+1, :] = I[r:2*r+1, :]
    imDst[r+1:h-r, :] = I[2*r+1:, :] - I[:h-2*r-1, :]
    imDst[h-r:,:]=np.matlib.repmat(I[h-1,:],r,1)-I[h-2*r-1:h-r-1,:]
    
    # col process
    I = np.cumsum(imDst, 1)
    imDst[:,:r+1] = I[:,r:2*r+1]
    imDst[:,r+1:w-r] = I[:,2*r+1:]-I[:,:w-2*r-1]
    imDst[:,w-r:] = np.matlib.repmat(I[:,w-1].reshape(-1,1),1,r)-I[:,w-2*r-1:w-r-1]
    return imDst

性能分析

本节使用正常的卷积局部求和操作与boxfilter局部求和进行对比分析，看看boxfilter性能到底如何。这里使用的卷积操作与这篇文章中的代码一致

利用卷积操作来进行局部求和，只需要将卷积核定义为如下形式即可

1
kernel = np.array([[1,1,1], [1,1,1], [1,1,1]])

这样就定义了一个3x3的局部求和卷积核，验证一下卷积局部求和与boxfilter的输出结果是否一致

1
2
3
4
imSrc = np.ones((8, 8))
kernel = np.array([[1,1,1], [1,1,1], [1,1,1]])
im_new = image_conv2d(imSrc, kernel)
print(im_new)

输出结果为

1
2
3
4
5
6
7
8
[[4. 6. 6. 6. 6. 6. 6. 4.]
 [6. 9. 9. 9. 9. 9. 9. 6.]
 [6. 9. 9. 9. 9. 9. 9. 6.]
 [6. 9. 9. 9. 9. 9. 9. 6.]
 [6. 9. 9. 9. 9. 9. 9. 6.]
 [6. 9. 9. 9. 9. 9. 9. 6.]
 [6. 9. 9. 9. 9. 9. 9. 6.]
 [4. 6. 6. 6. 6. 6. 6. 4.]]

可以看出与boxfilter输出结果相同。接下来以3x3的窗口大小，分别以不同大小的单位矩阵来模拟不同分辨率的图像，对比两种运算随着分辨率的提升运算效率的变化情况

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
# resolution define
resList = []
resList.append((32,32))
resList.append((64,64))
resList.append((128,128))
resList.append((256,256))
resList.append((512,512))
resList.append((640,480))
resList.append((800,600))
resList.append((1024,768))
resList.append((1280,960))
resList.append((1600,1200))
resList.append((2048,1536))
resList.append((2272,1704))
resList.append((2560,1920))
resList.append((3000,2000))
resList.append((3264,2488))
resList.append((4080,2720))
resList.append((4536,3024))

# convolution calculate
conv_stats = []
for res in resList:
    imSrc = np.ones(res)
    kernel = np.array([[1,1,1], [1,1,1], [1,1,1]])
    start = time.time()
    im_new = image_conv2d(imSrc, kernel)
    runtimes = time.time()-start
    conv_stats.append(runtimes)

# boxfilter calculate
bxf_stats = []
for res in resList:
    imSrc = np.ones(res)
    start = time.time()
    im_new = boxfilter(imSrc, 1)
    runtimes = time.time() - start
    bxf_stats.append(runtimes)

# plot
x = ['{}x{}'.format(res[0], res[1]) for res in resList]
plt.plot(x, conv_stats, label='convolution')
plt.plot(x, bxf_stats, label='boxfilter')
plt.title('Comparison of convolution and boxfilter')
plt.xlabel('radius')
plt.ylabel('runtime(sec)')
plt.xticks(np.arange(0, 20, step=2))
plt.legend()
plt.show()

测试结果如下

Resolution Convolution Runtimes(sec) Boxfilter Runtimes(sec)
32x32 0.015528 0.008734
64x64 0.023325 0.000000
128x128 0.088296 0.000972
256x256 0.351377 0.000971
512x512 1.396757 0.006795
640x480 1.637542 0.006794
800x600 2.556762 0.010676
1024x768 4.169978 0.019385
1280x960 6.543228 0.032032
1600x1200 10.234725 0.049505
2048x1536 16.729388 0.109683
2272x1704 20.630525 0.102891
2560x1920 26.146850 0.133951
3000x2000 31.713583 0.163045
3264x2488 43.213059 0.231047
4080x2720 59.047499 0.323232
4536x3024 72.816411 0.392182

将测试结果绘制曲线如下

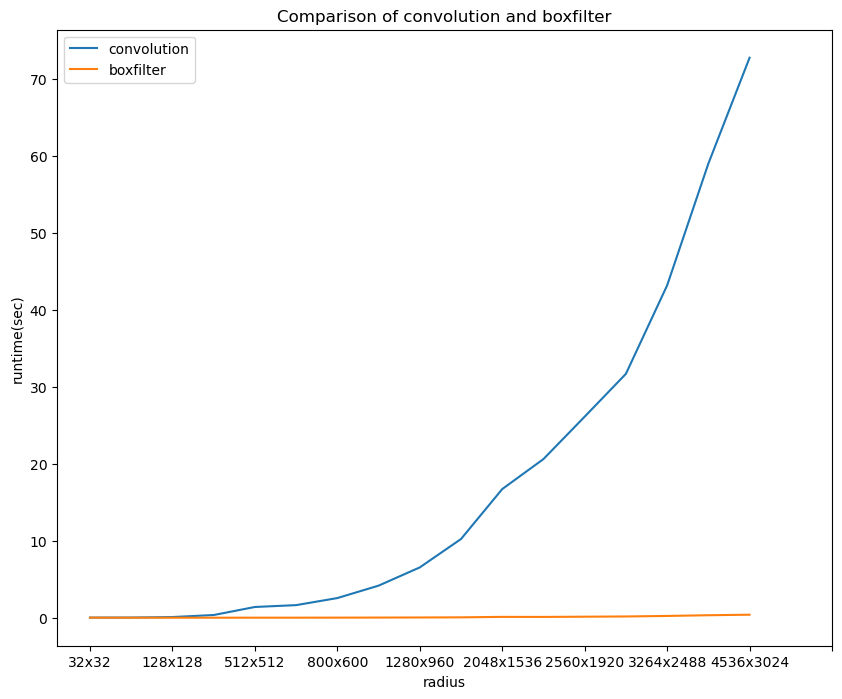
可以看出，在相同局部大小3x3情况下，boxfilter的性能提升是巨大的，随着分辨率的增大，普通的卷积运算耗时呈类似指数增长，而boxfilter的耗时虽然也有所增加，但是其增长程度远远小于分辨率的增长程度

3x3大小的局部窗口下，boxfilter的运算效率确实很高，那么随着半径的增大，boxfilter的效果如何呢？下面对不同分辨率下不同半径的窗口大小对boxfilter进行了对比测试

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
radList = [1,2,5,10,15,20,25,30,35,40,45,50]
bxf_stats = []
for res in resList:
    imSrc = np.ones(res)
    stat = {'res':res, 'times':[]}
    for rad in radList:
        if (rad*2+1)<res[0] and (rad*2+1)<res[1]:
            start = time.time()
            im_new = boxfilter(imSrc, rad)
            runtimes = time.time() - start
            stat['times'].append((runtimes, rad))
    bxf_stats.append(stat)

for i in range(len(bxf_stats)):
    x = [t[1] for t in bxf_stats[i]['times']]
    y = [t[0] for t in bxf_stats[i]['times']]
    plt.plot(x,y, label='{}'.format(bxf_stats[i]['res']))

plt.title('Compare boxfilters with different radius sizes')
plt.xlabel('radius')
plt.ylabel('runtime(sec)')
plt.legend()
plt.show()

测试结果如下

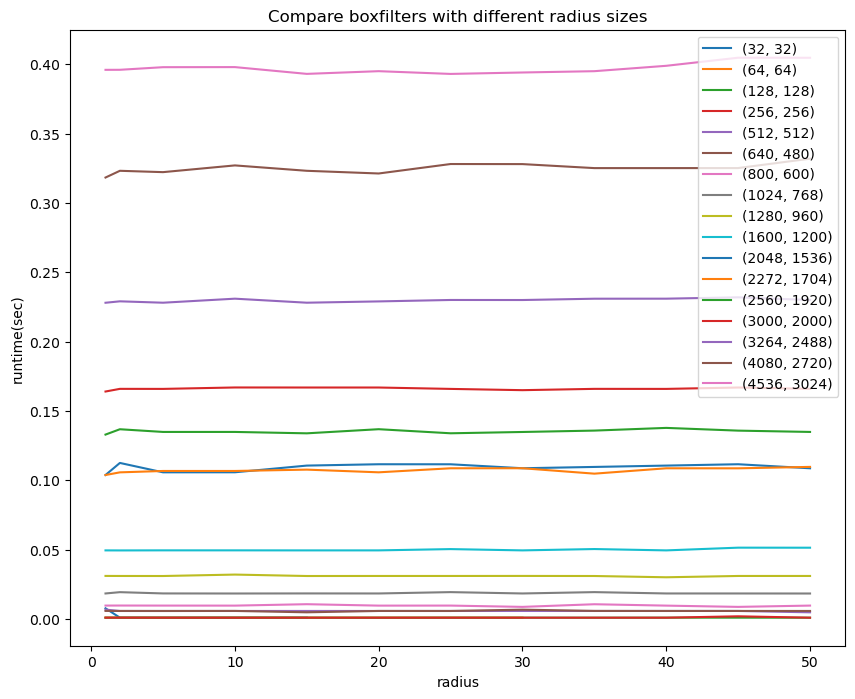
Amazing!!!

图中每条曲线代表一种分辨率下随着半径增大的运行时间变化情况，可以看出，固定分辨率的情况下，boxfilter的运算时间与半径大小几乎完全无关，只有分辨率增大，其运算时间才稍有增加。从boxfilter的计算原理可以理解，由于其计算过程只涉及到两次矩阵行方向与纵方向的累积求和运算，以及行方向、列方向的减法运算，因此当分辨率增大时，累积求和与减法运算的运算量会有所增加，但是由于其运算过程与半径大小的关系仅在考虑边界处的处理时，而且也是单次计算，因此半径大小带来的运算量增加与分辨率增加带来的运算量增加是非常小的