SharedMemocry优化矩阵乘法

发表于 | 分类于 |

巧妙的使用共享内存Shared memory，能够减少线程对全局内存Global memory的访问，提升CUDA程序在访存方面的性能。本文以矩阵乘法为例，通过对比不使用共享内存的普通矩阵乘法实现和使用共享内存的矩阵乘法优化版本，展示共享内存对程序性能的提升，并分析使用共享内存的条件和注意点

普通矩阵乘法

矩阵乘法的基本原理如下图所示

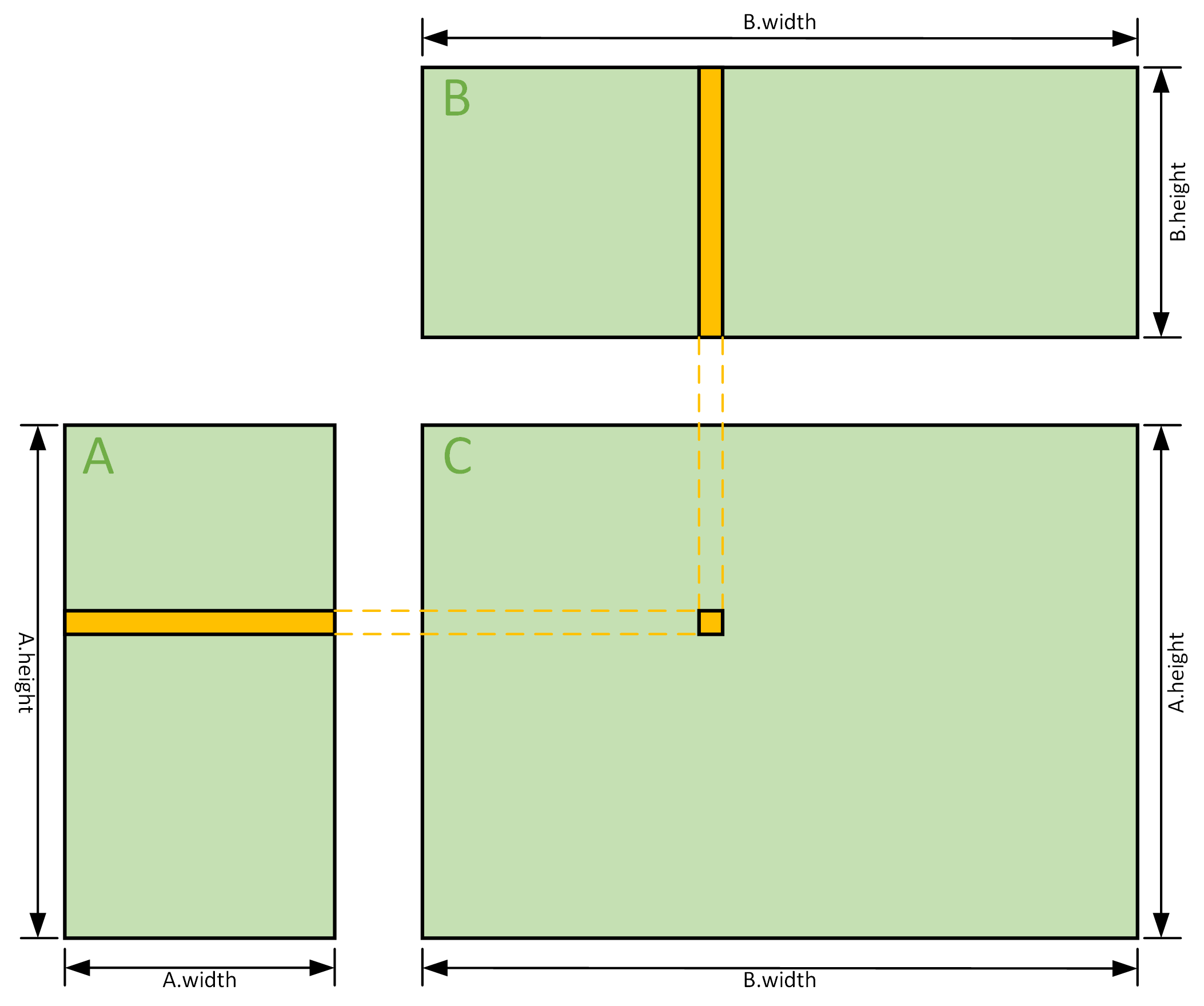
矩阵A与矩阵B相乘，得到矩阵C，相乘的一个重要条件是矩阵A的列数或者宽度与矩阵B的行数或者高度要相等，相乘得到的矩阵C的列数(宽度)与矩阵B的列数(宽度)相等，行数(高度)与矩阵A的行数(高度)相等，假设A为2x3的矩阵，B为3x4的矩阵，A和B相乘结果是C为2x4，注意这里的表述是行在前列在后。乘法中单个元素的对应关系是，C中的每个元素是A中对应行与B中对应列的逐元素相乘的累加和，如图中黄色部分，整个乘法过程可以抽象成一个两层循环，外层循环是C中每个元素位置的循环，内层循环是A的行与B的列的逐元素循环

普通矩阵乘法的示例代码如下

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
#include "cuda_runtime.h"
#include "device_launch_parameters.h"
#include <iostream>
#include <memory>
#include <string>

using namespace std;

#define MATRIX_A_WIDTH    1024
#define MATRIX_A_HEIGHT   1920
#define MATRIX_B_WIDTH    1280
#define MATRIX_B_HEIGHT   MATRIX_A_WIDTH
#define BLOCK_SIZE        16
#define MAT_ELEM_NUM(m)   (m.width * m.height)
#define MAT_SIZE(m)       (MAT_ELEM_NUM(m) * sizeof(float))

typedef struct {
    int width;
    int height;
    float *data;
} Matrix;

__global__ void mat_mul_kernel_v1(Matrix A, Matrix B, Matrix C)
{
    /* get row/col index */
    int row = blockDim.x * blockIdx.x + threadIdx.x;
    int col = blockDim.y + blockIdx.y + threadIdx.y;

    float value = 0.0;

    /* foreach element in A's row and B's col */
    for (int i=0; i<A.width; i++) {
        value += A.data[row * A.width + i] * 
                 B.data[i * B.height + col];
    }

    /* write sum value to C */
    c.data[row * C.width + col] = value;
}

static void MatMulKernel(Matrix A, Matrix B, Matrix C)
{
    Matrix d_A, d_B, d_C;

    d_A.width  = A.width;
    d_A.height = A.height;
    d_B.width  = B.width;
    d_B.height = B.height;
    d_C.width  = C.width;
    d_C.height = C.height;

    /* Alloc cuda mem for A, B, C */
    cudaMalloc(&d_A.data, MAT_SIZE(A));
    cudaMalloc(&d_B.data, MAT_SIZE(B));
    cudaMalloc(&d_C.data, MAT_SIZE(C));

    /* Copy mem from host to device */
    cudaMemcpy(d_A.data, A.data, MAT_SIZE(A), cudaMemcpyHostToDevice);
    cudaMemcpy(d_B.data, B.data, MAT_SIZE(B), cudaMemcpyHostToDevice);

    /* Create and invoke cuda kernel */
    dim3 threadsPerBlock(BLOCK_SIZE, BLOCK_SIZE);
    dim3 numBlocks(C.height / BLOCK_SIZE, C.width / BLOCK_SIZE);
    printf("call kernel with blocks{%d,%d} threads{%d,%d}\n", B.width / BLOCK_SIZE,         A.height / BLOCK_SIZE, BLOCK_SIZE, BLOCK_SIZE);
    mat_mul_kernel_v1<<<numBlocks, threadsPerBlock>>>(d_A, d_B, d_C);

    /* Copy mem from device to host*/
    cudaMemcpy(C.data, d_C.data, MAT_SIZE(C), cudaMemcpyDeviceToHost);

    /* Free cuda mem */
    cudaFree(d_A.data);
    cudaFree(d_B.data);
    cudaFree(d_C.data);
}

int main(int argc, char *argv)
{
    Matrix A, B, C;

    /* Initialize A,B,C and alloc memory for them */
    A.width = MATRIX_A_WIDTH;
    A.height = MATRIX_A_HEIGHT;
    A.data   = (float *)malloc(MAT_SIZE(A));

       B.width  = MATRIX_B_WIDTH;
    B.height = MATRIX_B_HEIGHT;
    B.data   = (float*)malloc(MAT_SIZE(B));

    C.width  = MATRIX_B_WIDTH;
    C.height = MATRIX_A_HEIGHT;
    C.data   = (float*)malloc(MAT_SIZE(C));

    MatMulKernel(A, B, C);

    free(A.data);
    free(B.data);
    free(C.data);

    exit(EXIT_SUCCESS);
}

程序中为每个block分配了16x16的二维线程数，block的大小由数据大小决定，每个线程计算C中的一个元素，通过线程的二维ID来确定当前线程计算C中的哪个元素

使用共享内存优化矩阵乘法

在普通矩阵乘法中，每个线程负责计算C中的一个元素，每个元素都会读取A中的一行和B中的一列。例如在计算C[2][1]时，线程1要读取一次A的第2行和B的第1列，在计算C[2][2]时，线程2要读取一次A的第2行和B的第2列，可以看到两个线程各进行了一次对A第二行的读取操作，由于从全局内存中读取数据是非常缓慢的，这种重复的读取如果可以被避免的话，能够有效提升程序性能。如下图所示，在优化的程序中，将最终要计算的结果矩阵C拆分成一个一个大小为 BLOCK_SIZE*BLOCK_SIZE的子矩阵$C{sub}$，每个线程块负责计算一个子矩阵$C{sub}$，而每个线程负责计算子矩阵中的每个元素。对A、B的读取也是以块为单位的，每次将读取的数据放入SharedMemory中，这样在计算完一个子矩阵$C_{sub}$时，对A的行读取、B的列读取能够从SharedMemory中获得，而不是每次都从全局内存中获取

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
#include "cuda_runtime.h"
#include "device_launch_parameters.h"
#include <iostream>
#include <memory>
#include <string>

using namespace std;

#define MATRIX_A_WIDTH    1024
#define MATRIX_A_HEIGHT   1920
#define MATRIX_B_WIDTH    1280
#define MATRIX_B_HEIGHT   MATRIX_A_WIDTH
#define BLOCK_SIZE        16
#define MAT_ELEM_NUM(m)   (m.width * m.height)
#define MAT_SIZE(m)       (MAT_ELEM_NUM(m) * sizeof(float))

typedef struct {
    int width;
    int height;
    int stride;
    float *data;
} Matrix;

__device__ void DevMatSetElement(Matrix m, int row, int col, float value)
{
    m.data[m.stride * row + col] = value;
}

__device__ float DevMatGetElement(Matrix m, int row, int col)
{
    return m.data[m.stride * row + col];
}

__device__ Matrix DevMatGetSub(Matrix m, int row, int col)
{
    Matrix sub;
    sub.width  = BLOCK_SIZE;
    sub.height = BLOCK_SIZE;
    sub.stride = m.stride;
    sub.data   = &m.data[m.stride * BLOCK_SIZE * row + 
                                    BLOCK_SIZE * col];
    return sub;
}

__global__ void mat_mul_kernel_v2(Matrix A, Matrix B, Matrix C)
{
    int blockRow = blockIdx.y;
    int blockCol = blockIdx.x;
    int row = threadIdx.y;
    int col = threadIdx.x;

    Matrix CSub = DevMatGetSub(C, blockRow, blockCol);

    float Cvalue = 0.0;

    /* foreach sub */
    for (int m=0; m<(A.width/BLOCK_SIZE); m++) {

        Matrix ASub = DevMatGetSub(A, blockRow, m);
        Matrix BSub = DevMatGetSub(B, m, blockCol);

        __shared__ float As[BLOCK_SIZE][BLOCK_SIZE];
        __shared__ float Bs[BLOCK_SIZE][BLOCK_SIZE];

        As[row][col] = DevMatGetElement(ASub, row, col);
        Bs[row][col] = DevMatGetElement(BSub, row, col);

        __syncthreads();

        /* foreach elem */
        for (int e=0; e<BLOCK_SIZE; e++) {
            Cvalue += As[row][e] * Bs[e][col];
        }

        __syncthreads();
    }

    DevMatSetElement(CSub, row, col, Cvalue);
}

static void MatMulKernel(Matrix A, Matrix B, Matrix C)
{
    Matrix d_A, d_B, d_C;

    d_A.width  = A.width;
    d_A.height = A.height;
    d_A.stride = A.stride;
    d_B.width  = B.width;
    d_B.height = B.height;
    d_B.stride = B.stride;
    d_C.width  = C.width;
    d_C.height = C.height;
    d_C.stride = C.stride;

    /* Alloc cuda mem for A, B, C */
    cudaMalloc(&d_A.data, MAT_SIZE(A));
    cudaMalloc(&d_B.data, MAT_SIZE(B));
    cudaMalloc(&d_C.data, MAT_SIZE(C));

    /* Copy mem from host to device */
    cudaMemcpy(d_A.data, A.data, MAT_SIZE(A), cudaMemcpyHostToDevice);
    cudaMemcpy(d_B.data, B.data, MAT_SIZE(B), cudaMemcpyHostToDevice);

    /* Create and invoke cuda kernel */
    dim3 threadsPerBlock(BLOCK_SIZE, BLOCK_SIZE);
    dim3 numBlocks(C.height / BLOCK_SIZE, C.width / BLOCK_SIZE);
    printf("call kernel with blocks{%d,%d} threads{%d,%d}\n", B.width / BLOCK_SIZE,         A.height / BLOCK_SIZE, BLOCK_SIZE, BLOCK_SIZE);
    mat_mul_kernel_v2<<<numBlocks, threadsPerBlock>>>(d_A, d_B, d_C);

    /* Copy mem from device to host*/
    cudaMemcpy(C.data, d_C.data, MAT_SIZE(C), cudaMemcpyDeviceToHost);

    /* Free cuda mem */
    cudaFree(d_A.data);
    cudaFree(d_B.data);
    cudaFree(d_C.data);
}

int main(int argc, char *argv)
{
    Matrix A, B, C;

    /* Initialize A,B,C and alloc memory for them */
    A.width = MATRIX_A_WIDTH;
    A.height = MATRIX_A_HEIGHT;
    A.stride = A.width;
    A.data   = (float *)malloc(MAT_SIZE(A));

    B.width  = MATRIX_B_WIDTH;
    B.height = MATRIX_B_HEIGHT;
    B.stride = B.width;
    B.data   = (float*)malloc(MAT_SIZE(B));

    C.width  = MATRIX_B_WIDTH;
    C.height = MATRIX_A_HEIGHT;
    C.stride = C.width;
    C.data   = (float*)malloc(MAT_SIZE(C));

    MatMulKernel(A, B, C);

    free(A.data);
    free(B.data);
    free(C.data);

    exit(EXIT_SUCCESS);
}

Performance

显卡 KernelVersion KernelLaunchTime(us)
GTX 730(sm_35) V1 2849372.820
GTX 730(sm_35) v2 2154518.019